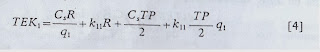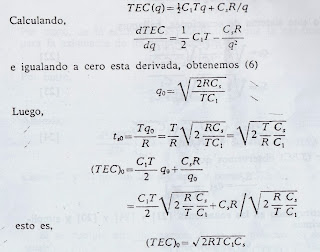Habiendo analizado e ilustrado las normas de decisión para la determinación de ¡as cantidades más económicas en el caso en que el
precio de compra está sujeto a una o dos bajas de precios, podemos
ahora generalizar estas normas para cualquier número de bajas de
precios.
lunes, 30 de diciembre de 2013
domingo, 29 de diciembre de 2013
jueves, 26 de diciembre de 2013
miércoles, 25 de diciembre de 2013
martes, 24 de diciembre de 2013
lunes, 23 de diciembre de 2013
MODELOS DE COMPRA-INVENTARIO CON DOS REBAJAS DE PRECIOS - II
Estas normas de decisión vamos a ilustrarlas con cinco ejemplos. El
lector deberá observar que estos ejemplos representan cada uno las
cinco situaciones posibles que pueden resultar del caso de dos rebajas
de precios. En el cuadro 9-1 damos los datos de estos cinco ejemplos.
domingo, 22 de diciembre de 2013
MODELOS DE COMPRA-INVENTARIO CON DOS REBAJAS DE PRECIOS - I
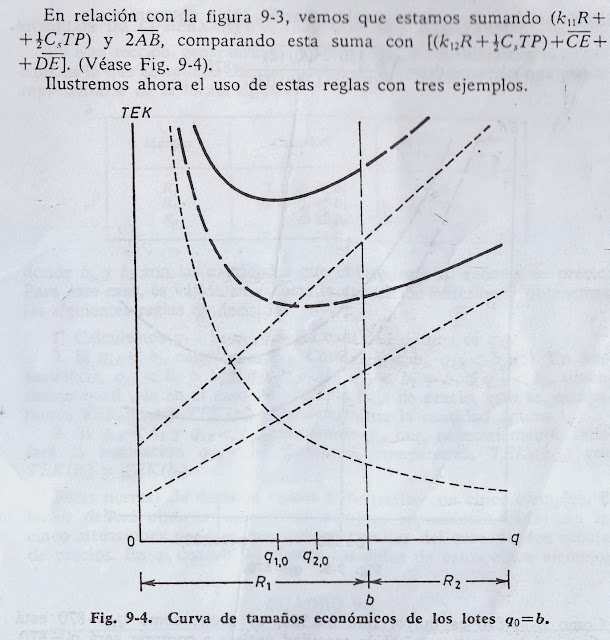
En esta sección, generalizamos un paso más, y consideramos la situación en la que se aplican dos descuentos de precios, situación que puede
representarse de la forma siguiente:
donde b1 y b2 son las cantidades que determinan las rebajas de precio. Para este caso, es válida en esencia la exposición anterior, y obtenemos las siguientes reglas de decisión:
donde b1 y b2 son las cantidades que determinan las rebajas de precio. Para este caso, es válida en esencia la exposición anterior, y obtenemos las siguientes reglas de decisión:
sábado, 21 de diciembre de 2013
MODELO DE COMPRA-INVENTARIO CON UNA REBAJA DEL PRECIO - Ejemplo 3
Ejemplo III.— En este ejemplo supongamos que mantenemos las
condiciones del ejemplo II, salvo que ahora la baja de precio no tiene
lugar hasta q = 3.000. Como antes,
viernes, 20 de diciembre de 2013
MODELO DE COMPRA-INVENTARIO CON UNA REBAJA DEL PRECIO - Ejemplo 2
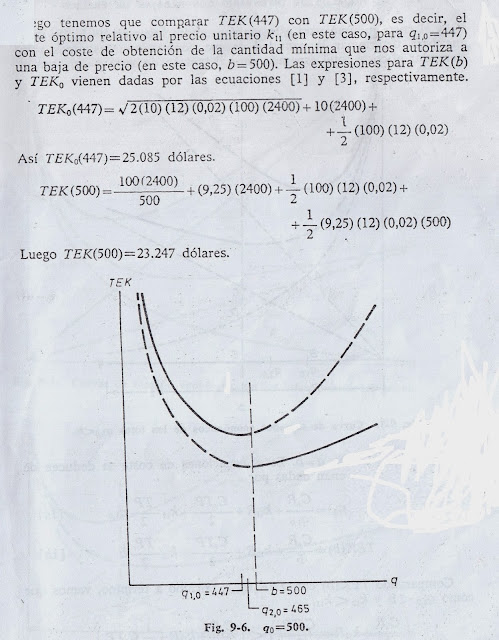
Ejemplo II.—La situación es diferente si el coste de preparación
es solo de 100 dólares, esto es, cuando Cs=100 dólares. Entonces,
Por tanto, como en este ejemplo TEK (500)< TEK 0 (447), la cantidad optima está determinada por la baja de precio, esto es, q0=500. Esta situación esta representada en la figura 9-6
Por tanto, como en este ejemplo TEK (500)< TEK 0 (447), la cantidad optima está determinada por la baja de precio, esto es, q0=500. Esta situación esta representada en la figura 9-6
jueves, 19 de diciembre de 2013
MODELO DE COMPRA-INVENTARIO CON UNA REBAJA DEL PRECIO - Ejemplo 1
Ejemplo I.— Un fabricante de motores debe comprar 2.400 piezas
de fundición al año. Suponemos que esta cifra es fija y conocida. Estas
piezas están sujetas a descuentos por cantidad, es decir, el precio es
menor para cantidades situadas dentro de ciertos márgenes. El problema consiste en determinar la cantidad óptima a comprar. Sean:
Calculamos q2.0 de acuerdo con la ecuación [2] y obtenemos
Calculamos q2.0 de acuerdo con la ecuación [2] y obtenemos
miércoles, 18 de diciembre de 2013
lunes, 16 de diciembre de 2013
MODELO DE COMPRA-INVENTARIO CON UNA REBAJA DEL PRECIO - II
domingo, 15 de diciembre de 2013
MODELO DE COMPRA-INVENTARIO CON UNA REBAJA DEL PRECIO - I
En esta sección consideramos una situación de compra típica en la
que se aplica un descuento por cantidad. Tal situación puede representarse así:
siendo b la cantidad a partir de la cual se aplica el descuento. Así, para cualquier cantidad comprada, qh en el margen R„ el coste total esperado TEKX vendrá dado por
y, análogamente, para cualquier cantidad q2, en el margen R,, el coste total esperado TEKZ será
siendo b la cantidad a partir de la cual se aplica el descuento. Así, para cualquier cantidad comprada, qh en el margen R„ el coste total esperado TEKX vendrá dado por
y, análogamente, para cualquier cantidad q2, en el margen R,, el coste total esperado TEKZ será
sábado, 14 de diciembre de 2013
ECUACIONES BASICAS DEL COSTE - II
Por tanto, el coste total para el período t es
Consideremos ahora una primera generalización para el caso en que el coste de compra esta sujeto a una alteración del precio.
Consideremos ahora una primera generalización para el caso en que el coste de compra esta sujeto a una alteración del precio.
ECUACIONES BASICAS DEL COSTE - I
Para cualquier valor del coste de compra unitario ku la situación
que acabamos de describir puede representarse gráficamente como se
hace en la figura 8-1. Además, como en el capítulo 8,
Por tanto, para cada serie, el número de piezas-meses en inventario vendrá dado por
Por tanto, para cada serie, el número de piezas-meses en inventario vendrá dado por
viernes, 13 de diciembre de 2013
MODELOS DE INVENTARIO CON REBAJAS DE PRECIOS - II
Como un coste unitario variable de fabricación o de compra es más
apropiado en el caso de piezas compradas (debido a los descuentos
según cantidad) nos referiremos desde ahora solo a piezas compradas,
lo que facilitará el estudio que sigue sin pérdida de generalidad.
El problema consiste, pues, en determinar:
- La frecuencia con que deberían comprarse las piezas.
- Cuántas unidades deberían comprarse cada vez.
jueves, 12 de diciembre de 2013
MODELOS DE INVENTARIO CON REBAJAS DE PRECIOS - I
En este capítulo consideramos una ciase de problemas de inventario en los que el coste unitario de fabricación o de compra es variable, situación típica en la compra de piezas sujetas a descuentos
según la cantidad comprada.
Aunque es posible elaborar esta generalización del problema de inventario para cada uno de los modelos analizados en el capítulo 8, solo lo haremos para el Modelo I de ese capítulo por ser este el que se utiliza con más frecuencia como punto de
partida.
Para parafrasear el problema del Modelo I (Cap. 8), consideremos
un fabricante que tiene que comprar o suministrar R unidades a un
ritmo constante durante un tiempo T. La demanda es, pues, fija y
conocida. No existen escaseces, por lo que el coste de escasez es infinito (es decir, usando la notación del Cap. 8, C2=oo). Los costes variables asociados al proceso de fabricación o de compra pueden designarse por (I):
Igual que en el capítuo 8, seamiércoles, 11 de diciembre de 2013
Caso práctico que utiliza el Modelo VI - Part 13
Por tanto, el valor de S que hace mínimo el coste total esperado es el
valor de S0 que satisface la inecuación [42] o las desigualdades
martes, 10 de diciembre de 2013
Caso práctico que utiliza el Modelo VI - Part 12
Por tanto, de las ecuaciones [35] y [36] se deduce que
TEC(S + \)=TEC(S)-r
Entonces, de la ecuación [37],
Entonces, de la ecuación [37],
lunes, 9 de diciembre de 2013
Caso práctico que utiliza el Modelo VI - Part 11
Nota 6.— En esta nota determinamos el valor de S que hace mínimo
el coste total esperado TEC, siendo
Sustituyendo S por (S-t-1) en la ecuación [35], tenemos
Sustituyendo S por (S-t-1) en la ecuación [35], tenemos
domingo, 8 de diciembre de 2013
jueves, 5 de diciembre de 2013
Caso práctico que utiliza el Modelo VI - Part 9
Nota 4.—En esta nota determinamos el valor de S que hace mínimo
el coste total esperado TEC, donde
El TEC tendrá un valor extremo relativo (máximo o mínimo) si
El TEC tendrá un valor extremo relativo (máximo o mínimo) si
miércoles, 4 de diciembre de 2013
Caso práctico que utiliza el Modelo VI - Part 8
Para cualquier número entero S' mayor que 5 y para cualquier número entero S" menor que S0 se verificarían las inecuaciones [29], ya
que P{r^S0) no es decreciente para valores crecientes de So. De aquí
que si se verifica la inecuación [29] (8)
Hemos encontrado así el valor de S que hace mínimo el coste total esperado, es decir, el S0 que satisface las inecuaciones [29]. Estas inecuaciones pueden ponerse de forma que den
Hemos encontrado así el valor de S que hace mínimo el coste total esperado, es decir, el S0 que satisface las inecuaciones [29]. Estas inecuaciones pueden ponerse de forma que den
martes, 3 de diciembre de 2013
lunes, 2 de diciembre de 2013
Caso práctico que utiliza el Modelo VI - Part 6
Nota 2.—En esta nota determinamos los valores de q y S que hacen mínimo el coste total esperado, siendo
e igualando a cero (7) estas derivadas parciales y simplificando, obtemos
Obsérvese que para q0 y S0 el coste de formación de almacenamiento es otra vez igual al coste de instalación. Además, conviene observar que la razón entre el coste de transporte de los excedentes y el
coste de "transporte" del déficit es inversamente proporcional al
coste unitario de excedente y de falta de existencias.
domingo, 1 de diciembre de 2013
Caso práctico que utiliza el Modelo VI - Part 5
Nota 1.—En esta nota determinamos el valor de q, que llamamos go. y hace mínimo el coste total esperado TLC (</), siendo
(Obsérvese que en este modelo el coste de almacenamiento es igual al coste de instalación.)
(Obsérvese que en este modelo el coste de almacenamiento es igual al coste de instalación.)
sábado, 30 de noviembre de 2013
Caso práctico que utiliza el Modelo VI - Part 4
Igual que antes, preparamos los cálculos que aparecen en el cuadro 8-8. Entonces, el valor óptimo de S es 5, ya que
Por tanto, el coste anual total, en dólares, asociado a la política lanzar una serie cada 2 meses es
Análogamente, podrían hacerse los cálculos para una política de producir cada 3 meses. El resultado (que puede comprobarse por el lector) daría un coste anual total mínimo de 7.109 dólares. Podemos resumir los resultados de la forma siguiente:
Cálculos ulteriores para períodos mayores revelarían, en este caso, costes anuales crecientes. Es evidente, pues, que deberían producirse en cada uno de los otros meses unidades suficientes para que el stock inicial esté compuesto por cinco unidades.
Por tanto, el coste anual total, en dólares, asociado a la política lanzar una serie cada 2 meses es
Análogamente, podrían hacerse los cálculos para una política de producir cada 3 meses. El resultado (que puede comprobarse por el lector) daría un coste anual total mínimo de 7.109 dólares. Podemos resumir los resultados de la forma siguiente:
Cálculos ulteriores para períodos mayores revelarían, en este caso, costes anuales crecientes. Es evidente, pues, que deberían producirse en cada uno de los otros meses unidades suficientes para que el stock inicial esté compuesto por cinco unidades.
Suscribirse a:
Entradas (Atom)