Caso práctico que utiliza el Modelo VI - Part 4

Igual que antes, preparamos los cálculos que aparecen en el cuadro 8-8. Entonces, el valor óptimo de S es 5, ya que

Por tanto, el coste anual total, en dólares, asociado a la política lanzar una serie cada 2 meses es

Análogamente, podrían hacerse los cálculos para una política de producir cada 3 meses. El resultado (que puede comprobarse por el lector) daría un coste anual total mínimo de 7.109 dólares. Podemos resumir los resultados de la forma siguiente:

Cálculos ulteriores para períodos mayores revelarían, en este caso, costes anuales crecientes. Es evidente, pues, que deberían producirse en cada uno de los otros meses unidades suficientes para que el stock inicial esté compuesto por cinco unidades.

Caso práctico que utiliza el Modelo VI - Part 3

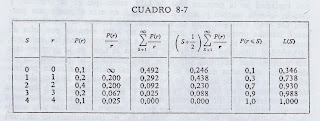
Luego, utilizando el cuadro 8-7, elegimos aquel valor de S que satisfaga la condición

El coste, en dólares, de almacenamiento total esperado al mes asociado a S=3 se halla utilizando la ecuación [17]:

Para obtener el coste, en dólares, pertinente de producción (4) debemos sumar el coste de establecimiento, 

225 + 350 = 575. 

El coste total anual, en dólares, óptimo para cada serie mensual sería, por tanto, 

(12) (575) = 6.900.

Ahora queremos determinar el coste anual óptimo asociado a la política de fabricar un serie cada 2 meses. En primer lugar, es necesario una distribución de las necesidades en un período de 2 meses. La probabilidad de obtener necesidades nulas en un período de 2 meses es (0,1) (0,1)=0,01, esto es, el producto de las probabilidades de necesitar cero unidades cada mes. Análogamente, podemos calcular (siendo P la probabilidad asociada a un período de 2 meses y P la probabilidad asociada a un período de 1 mes) (5):

Caso práctico que utiliza el Modelo VI - Part 2

Supongamos que la distribución de las necesidades mensuales mostrada en el cuadro 8-6.

Determinemos el volumen óptimo de bandas a fabricar mensual- mente. Empecemos preparando un cuadro con los datos y cálculos necesarios (cuadro 8-7).

Después, calculemos

Caso práctico que utiliza el Modelo VI - Part 1

Caso práctico que utiliza el Modelo VI—Hasta ahora los ejemplos han sido muy sencillos y, quizá, poco realistas, por lo que puede ser de utilidad el aplicar uno de los modelos en un caso real. El modelo usado será el VI. La sociedad implicada en este caso fabrica una pieza utilizad.", de forma amplia en máquinas, especialmente en automóviles, aeroplanos, tractores, etc. 

Es una pieza relativamente pequeña que se vende a un coste bajo. El proceso de fabricación está dividido en dos fases. 

En la primera, se da forma a la materia prima, se la recubre de una aleación y es laminada. 

En la segunda, las piezas se forjan y se terminan. Las razones de esta división en dos fases son: a) Las piezas producidas tienen muchos tamaños y tipos, b) Muchos de estos tamaños y tipos proceden de las mismas bandas de metal. Por tanto, existe mucha menos variedad en la primera fase de fabricación que en la segunda, y esta es la más costosa y larga. 

Los retrasos en esta segunda fase pueden ser muy costosos para la sociedad, por lo que se mantienen en stock bandas preparadas de forma que no haya retrasos por falta de bandas. Debido al alto coste asociado a los retrasos en las entregas, la sociedad intentaba mantener en almacén al final de la primera fase del proceso una cantidad suficiente para cubrir el 95 por 100 de las demandas esperadas durante el período transcurrido entre la producción de las series de bandas. Se vio que esto equivalía a asignar al coste mantenimiento (3). 

El problema consistía en determinar la frecuencia con que deberían hacerse las series de producción de bandas y la cantidad de cada serie. Por razones prácticas, es conveniente lanzar una banda determinada una vez cada 1, 2, 3 o más meses, pero no, p. ej., cada 2 ó 5 semanas. Para simplificar el cálculo, y con ello exponer mejor el método empleado, se utilizarán datos simplificados. En primer lugar, los costes en dólares son los siguientes:

MODELO VI - III

Utilizando el método descrito en la Nota 6 al final de este capítulo, podemos determinar que el valor óptimo de S es aquel que satisface la condición

Solución al ejemplo VI.—Para facilitar el cálculo es conveniente preparar una tabla de valores como la que aparece en el cuadro 8-5. Después calcularemos:

A partir de este cuadro, podemos elegir el valor de S que satisfaga la condición

Utilizando la ecuación de coste 17, podemos calcular el coste total

esperado asociado a un nivel de almacenamiento de tres unidades.

7EC( 3)1 [0,1) (3) + (0,2) (2,5) + (0,2) (2,0) + (0,3) (1,5) H

+ 1 [(0,1) (9/8) +(0,1) (9/10)1 + 201(0,1) (1/8) +
+ (0,1) (4/10)] =1,65+ 0,2025 + 1,05 = 2,9025 dólares.

MODELO VI - II

Ecuación de coste y solución analítica.—Consideremos primero el coste asociado a la situación representada en la figura S-6a, en la que, para un valor dado de r, el número medio de unidades en almacén durante el período del ciclo es

Por tanto, como P(r) es la probabilidad de necesitar r unidades discretas, el coste esperado correspondiente al mantenimiento en stock de este número de unidades es C,P(r)[S-(r/2)]. El coste total esperado asociado a la figura 8-6¿z se obtiene sumando todos los valores

Consideremos ahora la figura 8-66, donde r > S. Tengamos primero en cuenta aquella parte del período durante la cual no hay inexistencias. La parte del período en la que ocurre esto es t1/(ti + t2, que es igual a S/r, como se ve acudiendo a relaciones triangulares de semejanza. El volumen medio almacenado es S/2. El coste de mantenimiento en almacén para cada r durante esa parte del período es

Y la parte del período durante la cual hay déficit es (r-S)/r. El déficit medio es (r—S)/2. Luego, para cada r el coste de inexistencias es

Combinando estos componentes, tenemos la ecuación de coste siguiente:

MODELO VI - I

Ejemplo VI. —Un fabricante desea saber cuál es el nivel óptimo de stock de una cierta pieza de la que se reciben pedidos a un ritmo relativamente constante, pero no de un volumen constante. El fabricante recibe sus pedidos de forma prácticamente inmediata y hace sus pedidos a principios de cada mes. El estudio de la demanda revela que

las probabilidades del cuadro 8-4 corresponden a diversas exigencias mensuales. El coste de mantenimiento en stock de una unidad un mes es de un dólar, y el coste de un déficit de una unidad al mes es de 20 dólares.

MODELO VI

Este problema es similar al considerado en el Modelo III, con la diferencia de que las retiradas de los stocks son continuas. En este caso se supone que la tasa de retirada es virtualmente constante. Este tipo de situación puede representarse gráficamente, como se hace en la figura 8-6

Solución al ejemplo V

Solución al ejemplo V.—Primero, determinemos el valor óptimo de S\ que es el valor que satisface la condición

podemos resolver sustituyendo para hallar el valor óptimo de q,

Ecuación del coste y solución analítica

En primer lugar enumemos las características conocidas de la situación:

En la Nota 5 al final de este capítulo se da justificación detallada de esta solución.

MODELO V

Este problema tipo es similar al anterior con la importante diferencia de que el plazo de entrega es ahora significativo, es decir, hay que tener en cuenta el tiempo transcurrido entre el momento del pedido y la entrega de los bienes. 

Ejemplo.—El propietario de una tienda hace pedidos diarios de bienes que serán entregados 7 días más tarde (es decir, el plazo de entrega es de 7 días). En un determinado día, el propietario tiene un stock de 10 lib, y en los días anteriores ha hecho pedidos para la entrega de 2, 4, 1, 10, 11 y 5 lib, en este orden. Para facilitar los cálculos, supongamos condiciones similares a las del último ejemplo, o sea,

MODELO IV - Part 2

Interpretación del óptimo de S.—La ecuación F(S)=C2j(Ci + C¿ puede escribirse Cz/C, = [F(S)]/[l-F(S)] y tiene, por tanto, una interpretación interesante, a saber: bajo las condiciones óptimas, la relación entre la probabilidad de que la demanda sea menor que el nivel de almacenamiento óptimo y la probabilidad de que sea mayor es igual a la razón entre el coste de inexistencias unitario y el coste de mantenimiento unitario.

MODELO IV - Part 1

El problema tipo es el mismo que el de la última sección, salvo que ahora se supone que los niveles de stock son cantidades continuas, en lugar de discretas. De aquí que la probabilidad de que un pedido esté

Ecuación del coste.—En este caso, la ecuación de coste es similar a la del problema del Modelo III. En la ecuación [10], P(r) se sustituye por f(r) dr y la suma por una integral, y queda

En este caso, la solución analítica demuestra que (véase nota 4) el coste total esperado es mínimo para el valor de S que satisface la condición

MODELO III - Part 4

Estimación del coste de inexistencias.—La solución analítica de este problema puede utilizarse para determinar el margen de valores que se da a la falta de piezas. Supongamos, p. ej., que en los casos anteriores no conocíamos el coste de inexistencias, pero sí conocíamos que la política de los directivos era la de mantener un nivel de almacén de tres piezas. Podemos preguntarnos para qué valores de C2 es S0= 3. Esta pregunta puede contestarse de la forma siguiente:

MODELO III - Part 3

Solución por enumeración.

Podemos aplicar la ecuación [10] al ejemplo III y calcular el coste total esperado asociado a los niveles de stock probables (esto es, de 0 a 5, ya que los datos indican que no existe probabilidad de más de cinco averías). En el ejemplo, supondremos que el coste de no utilizar una pieza es simplemente su coste de compra, va que los costes de almacenamiento son insignificantes. Por tanto, Ci"=500 $. Se supone que el coste de escasez C2 es 10.000 S y consiste en el coste del tiempo de inactividad más el de producción de la pieza encargada. Aplicando la ecuación [10] a cada nivel de stock, obtenemos:

MODELO III - Part 2

Ecuación del coste.—La ecuación del coste (esto es, un modelo simbólico) para este tipo de problema puede deducirse como sigue. Supongamos que para cualquier cantidad en stock S, se utilizan r unidades. Para un determinado período de tiempo, el coste de mantenimiento de S unidades en stock es: 1. (S-r)C,, siendo r<5 data-blogger-escaped-2.="" data-blogger-escaped-de="" data-blogger-escaped-donde="" data-blogger-escaped-el="" data-blogger-escaped-en="" data-blogger-escaped-es="" data-blogger-escaped-esto="" data-blogger-escaped-igual="" data-blogger-escaped-menor="" data-blogger-escaped-mero="" data-blogger-escaped-n="" data-blogger-escaped-o="" data-blogger-escaped-que="" data-blogger-escaped-r-s="" data-blogger-escaped-r="" data-blogger-escaped-stock="" data-blogger-escaped-unidades="" data-blogger-escaped-usadas="">S (esto es, el número de unidades necesarias es mayor que el número de unidades en stock). Nosotros no sabemos de antemano cuál va a ser el valor de r, pero cada valor de r tiene su correspondiente probabilidad, P{r). Entonces, el coste esperado correspondiente a un determinado valor de r es:

Para obtener el coste total esperado, debemos sumar todos los costes esperados, es decir, los costes asociados a cada valor posible de r. El coste total esperado TEC. asociado a un nivel de stock de S unidades, viene dado por la ecuación

MODELO III - Part 1

El problema tipo considerado ahora introduce, además de un coste de inexistencias finito (como en el Modelo II), los conceptos siguientes (1): Demandas variables e input estimadas; unidades discretas, distribución discontinua en el tiempo de salidas y entradas de almacén a un ritmo discontinuo; tiempo del ciclo de sustitución constante y conocido. 

Ejemplo .—Una empresa de electricidad va a pedir un nuevo generador. Una de las piezas esenciales de este generador es muy complicada y costosa y no es rentable solicitarla separada del generador, pues cada pieza está construida para un generador determinado y no sirve para otro. La empresa desea saber cuántas piezas de recambio deberían pedirse con cada generador. Se dispone de la siguiente información: El coste de la pieza (si se pide junta con el generador) es de 500 dólares. Si se necesita una pieza de recambio (por avería de la pieza anterior) y no se dispone de ella, el generador queda totalmente inútil. El coste del generador mientras permanece inactivo, más el de la pieza encargada, es de 10.000 dólares. Un estudio de la conducta de piezas análogas en generadores similares da la información presentada en el cuadro 8-2 basado en 100 generadores.

Modelo II - Part 2

Sustituyendo los valores de t1 y t2, tenemos:

De la ecuación [5] pueden obtenerse los valores óptimos de q y S,como se hace en la nota 2 al final de este capítulo. Los resultados

Si comparamos los resultados de los Modelos I y II, observamos que : 1. Las ecuaciones [2], [3] y [4] pueden obtenerse haciendo que C2 se haga infinitamente grande en las ecuaciones [61, [8] y m El resultado no es extraño, ya que el Modelo I es un caso particular del Modelo II.

Luego el coste total esperado asociado a decisiones basadas en el Modelo II es menor que el basado en el Modelo I.

Modelo II - Part 1

Este problema tipo es similar al estudiado en el Modelo I, con la única diferencia de que ahora se supone que pueden existir inexistencias (es decir, que el coste de inexistencias no es infinito) 

Ecuación del coste y se solución analítica: 

La situación puede representarse gráficamente como en la figura 8-3, donde S es el nivel de almacenamiento al principio de cada intervalo. Utilizando una relación geométrica sencilla (triángulos semejantes), observamos que

El número medio de unidades en almacén durante ít es S/2; por tanto,

De forma similar, el número medio de unidades de inexistencias durante t2 es (q - S)/2. Por tanto,

De aquí se deduce que el coste total esperado durante T es

Modelo I (Part 2)

Examinando la ecuación [1], vemos que los dos términos del segundo miembro representan los costes totales de almacenamiento y los costes totales de instalación, respectivamente. El primero de estos términos aumenta al aumentar el tamaño de la serie, y el segundo disminuye, luego la solución del problema consiste en encontrar el valor de q (tamaño de la serie), o sea q0, que haga mínima la suma de estos dos costes (Fig. 8-2).

Puede obtenerse analíticamente una solución utilizando el cálculo diferencial elemental, como se hace en la nota 1 al final de este capitulo. El valor óptimo de q, representado por q0, es

y el correspondiente óptimo ts y mínimo TEC son:

Modelo I (Part 1)

Consideremos un fabricante que tiene que suministrar a sus clientes R unidades, a un ritmo constante, durante el tiempo T. La demanda es, pues, fija y conocida. No hay inexistencias; por tanto, el coste de estas es infinito (es decir, C2—oc). Los costes variables asociados al proceso de fabricación son: C1 = coste de mantenimiento de una unidad en almacén durante una unidad de tiempo. C2 = coste de instalación por serie producida. El problema del fabricante consiste en determinar: 

1. La frecuencia con que debe hacer las series de producción. 
2. El número de unidades que deben fabricarse por serie.

Ecuación del coste y solución analítica.—La situación que acabamos de describir puede representarse gráficamente en la figura 8-1.

Clasificación de las características de los problemas del Inventario

Cuadro

Consideraremos solamente los modelos de unos pocos problema?, característicos, pero la comprensión del método utilizado en la resolución de estos problemas facilitará la resolución de otros tipos distintos. A continuación, damos una lista de los símbolos utilizados a lo largo del análisis de los modelos de inventario de la parte VI:

INTRODUCCION - II

Estos costes pueden permanecer constantes o pueden variar en función del tiempo (p. ej., el coste correspondiente a un retraso en la entrega durante una estación del año puede ser mayor que este mismo coste en otra época, o en función del número de unidades (p. ej:, el coste de almacenamiento por unidad puede variar con el número de unidades almacenadas). Además de las variables relativas al coste, hay que tener en cuenta otras dos clases importantes de variables: las de la demanda y las de los pedidos. 

• Variables relativas a la demanda.—La demanda puede ser conocida o desconocida. En el primer caso, puede ser constante o variable por unidad de tiempo. Las cantidades de mercancías pueden tener valores discretos (p. ej., número de automóviles) o continuos (p. ej., número de toneladas de petróleo). Además, la retirada de mercancías de almacén puede ser discontinua en el tiempo (como la venta de helados en los campos de fútbol) o continua (la venta de helados en un aeropuerto). Por último, también puede ser constante o variable el ritmo de las retiradas de almacén. 
• Variables relativas a los pedidos.—El plazo de entrega puede ser instantáneo (p. ej., un pedido de leche en un almacén) o puede ser considerable. Los momentos en los que se hacen los pedidos pueden ser fijos o variables. La entrega de mercancías a almacén puede hacerse en cantidades discretas o continuas y constantes o variables. Por último, las llegadas a almacén pueden ser continuas o discretas y hacerse a un ritmo constante o variable. Son posibles muchos otros tipos de combinaciones, pero los enumerados dan ya lugar a varios miles de problemas posibles. Las características enumeradas se presentan en el cuadro 8-1 de forma que quede identificado cada problema tipo.

INTRODUCCION - I

Este capítulo quiere ser una introducción al tipo de análisis que da lugar a modelos simbólicos de los procesos de inventario. No se intenta desarrollar aquí un modelo general, que cubra una gran diversidad de problemas, sino solo considerar una sucesión de problemas sobre inventarios relativamente sencillos y los modelos específicos aplicables a estos problemas. Se sacrifica la generalidad, a cambio de dar un carácter práctico al estudio, ya que el resultado de este enfoque elemental debe ser unas herramientas de fácil aplicación. 

Además, se concede más importancia a las aplicaciones que a las derivaciones o deducciones. La clase general de problemas que vamos a considerar implica la adopción de decisiones relativas a los niveles de inventario. Estas decisiones pueden clasificarse de la forma siguiente: 

1. El momento en que se hacen los pedidos está fijado y hay que determinar la cantidad a pedir. 
2. Hay que determinar tanto el momento de hacer el pedido como las cantidades.

El problema de la investigación es encontrar la manera de hacer óptimas tales decisiones. Una decisión óptima es aquella que hace mínima la suma de los costes asociados al proceso de almacenamiento. Estos costes son de tres tipos: 

1. Coste de obtención de los bienes, a través de la compra o la fabricación. (Coste de instalación.) Es un coste fijo por serie y, por tanto, un coste variable por unidad. 
2. Coste de mantenimiento de una unidad en almacén. Incluye, entre otros, el coste del dinero gastado en la producción de la pieza, almacenamiento, manipulación, depreciación, daños, seguros e impuestos. 
3. Coste de inexistencias. Es el coste correspondiente a los retrasos en atender los pedidos o a la imposibilidad de atenderlos.

¿Qué quedó fuera?

El tema de sistemas productivos es muy extenso y, por falta de espacio, no se puede cubrir ampliamente en este capitulo. Sin embargo, se refiere al lector a las publicaciones pertinentes donde se presen- tan los temas faltantes. El caso de sistemas de producción estáticos de varios productos, con demandas determinísticas, costos cóncavos de producción (que consideran costos fijos) y restricciones en la capacidad de producción, ha sido estudiado por Maxwell [93] y Magee y Boodman [19] . Los procesos de producción con demanda aleatoria estática y horizonte de planeación de varios periodos, han sido estudiados como casos particulares de los procesos markovianos de decisión (ver el capítulo 5, de este volumen) por Manne [44, 45, 115], Hadley y Whitin [12] y Hanssman [14]. Este último también ha estudiado dichos procesos cuando existen varias fases deproducción (verHanssman [112]). Los procesos de producción estáticos con demanda constante determinística y varias fases de producción se han analizado en Crovvston, et al [111] Johnson [114] y Taha y Skeith [118] .

El problema dinámico de producción con cambio en los niveles de la fuerza de trabajo y demanda conocida ha sido estudiado para el caso de costos variables, por Zangwill [56] , Holt, et al [133] , Hanssman y Hess [131] , Taubert [144] y Lippman, et al [42,43] . Otros enfoques de planeación agregada de la producción lo han proporcionado Jones [134] y Bowman [120, 121]. Algunos modelos determinísticos adaptativos para el control de la producción han sido investigados por Magee y Boodman [19] y Hanssman [131] . Modelos dinámicos determinísticos de producción Para varios productos con costos no lineales han sido descritos por Lasdon y Terjung [137] , Bergstrom y Smith [119] , Denzler [124], Manne [45] , Dzielinski, Baker y Manne [125] y Dzielinski v Gomory [126],

Procesos dinámicos, estocásticos

Se presenta a continuación un modelo markoviano de decisión (ver el capítulo 5 de este volumen), o programación dinámica estocástica, de un sistema de producción de un solo producto, cuya demanda es aleatoria, con distribución de probabilidad conocida, con un horizonte de planeación finito de n {n > 0) periodos, y una sola fase de producción. Se permite diferir la demanda a periodos futuros a un cierto costo penal. 

Sea Xt la tasa de producción en el periodo í, /, el inventario neto al finalizar el periodo t, kt {Xt, /,) la función (no necesariamente lineal) de producción, almacenamiento y penal durante el periodo t, D, la variable aleatoria que denota la demanda en el periodo t, con distribución de probabilidad conocida <¡>t {Dt). La serie de demandas Dlt D2, ...,£„ son variables mutuamente independientes. Sea/, (/) el costo mínimo esperado para los periodos t, t + 1, . - . , n cuando / es el inventario neto al principio del periodo t, (t = l, 2, ..., n). 

Entonces

La condición inicial se define como/, + ,(/) = 0. Para resolver la anterior función recursiva (por cierto bastante difícil), se puede utilizar un enfoque de salida a entrada (ver capítulo 5, volumen 1), empezando con el periodo n, después el n - 1, y así hasta llegar al periodo 1

Chames, Cooper y Symonds [110] han tratado este tipo de problemas para costos de producción, almacenamiento y penal del tipo lineal, por medio de la programación estocástica restringida (ver volumen 2, capítulo 6). Chames, Cooper y Symonds [110] han tratado este tipo de problemas para costos de producción, almacenamiento y penal del tipo lineal, por medio de la programación estocástica restringida (ver volumen 2, capítulo 6).

Procesos dinámicos, no lineales, determmísticos - Ejemplos - Part 3

A continuación se extiende el algoritmo de Zangwill [148] para permitir demanda diferida a un costo penal. En este caso la fución de costo es

donde

La función rccursiva sigue siendo